从TSJCTF & Codegate的两道crypto题中学习新姿势

0x00 背景

周末的时候参加了TSJCTF和codegate的比赛，感觉其中有两道题思路比较新颖，有一些新的知识值得学习，记录一下以便日后翻阅。

0x01 TSJCTF Signature

Category: Crypto
Solve: 2/428

源码：

from fastecdsa.curve import secp256k1 as CURVE
from Crypto.Cipher import AES
from hashlib import sha256
from secrets import randbelow

d = randbelow(CURVE.q)
P = d * CURVE.G


def sign(z):
    k = d ^ z
    r = (k * CURVE.G).x
    s = pow(k, -1, CURVE.q) * (z + r * d) % CURVE.q
    return r, s


messages = [
    "https://www.youtube.com/watch?v=16M9oC-a5bY",
    "https://www.youtube.com/watch?v=QDadz5JZCw8",
    "https://www.youtube.com/watch?v=kyNh7KnsTN0",
    "https://www.youtube.com/watch?v=Lqn42JJxS3I",
    "https://www.youtube.com/watch?v=dQw4w9WgXcQ",
    "https://www.youtube.com/watch?v=1Gw_-E784l0",
]

for m in messages:
    z = int(sha256(m.encode()).hexdigest(), 16)
    print(z, *sign(z))


from secret import flag

msg = f"Congrats! This is your flag: {flag}"
key = sha256(str(d).encode()).digest()[:16]
cipher = AES.new(key, AES.MODE_CTR)
print(cipher.encrypt(msg.encode()))

可以看出，本题采用了secp256k1作为曲线实现了一个有漏洞的ecdsa，分别对五个消息进行了签名，并且提供了它们的签名。

以往来看遇到的脆弱的ecdsa问题基本都出现在nonce上，最经典的就是使用了bias nonce，也就是nonce的bit数相较于q比较小，这就造成了当人们收集到很多签名的时候可以将求解d转化为求解hnp。

但本题使用的并不是bias nonce，可以看出它的nonce是由d ^ z产生的(也就是d xor z)，虽然与q的bit数相差不多，但这样的nonce在attacker获取到很多签名之后也是可以泄露d的，接下来我们来推导一下这个过程：

首先我们知道：

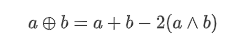
那么对于签名过程：（省略了mod q）

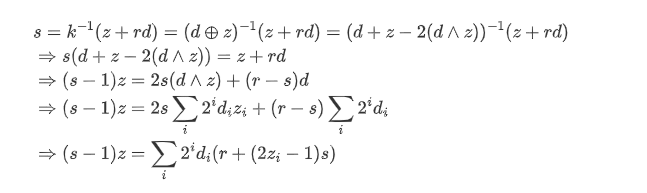
在正常情况下，我们如果收集256组签名，那么可以直接解线性方程组求出di，也就是d的每一个bit即可恢复d，但在这里，我们的0<= di <= 1，因此可以转化为求解svp即可。

主要方程：

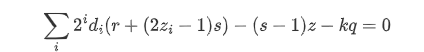
具体构造如下：

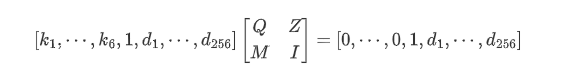
其中：

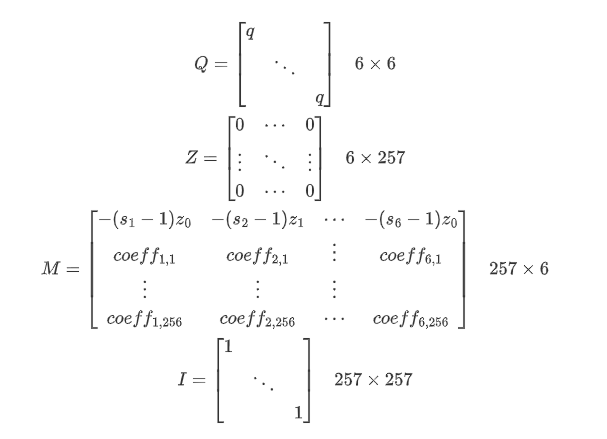
对矩阵

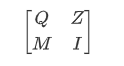
做LLL，我们可以知道目标向量即是LLL之后的一个行向量，遍历所得到的所有行，若该行的第7个元素是1，而且从第7个以后的元素都是0或1，那么这一行大概率就是包含d所有256位比特信息的一行，因此可以恢复出d，恢复之后即可拿到key，但是由于这个是AES-CTR模式，还需要一个nonce，刚好题目中给了明文的第一个block，那么利用AES-ECB模式对plantext_block0 ^ ciphertext_block0进行解密即可获得nonce。之后就可以正常解密了。

exp:

from pwn import *
from Crypto.Cipher import AES
from hashlib import *
from fastecdsa.curve import secp256k1 as CURVE

with open('/mnt/f/ctf/play/chall (1)/output.txt', 'r') as f:
    data = f.readlines()
    sigs = []
    for vec in data[:6]:
        z, r, s = map(int, vec.strip().split())
        sigs.append((z, r, s))
    c = data[-1].strip()
    c = eval(c)

m = 6
n = 257

UL = matrix.identity(m) * CURVE.q
UR = matrix.zero(m, n)
DR = matrix.identity(n)

main_mat = []
for i in range(6):
    z, r, s = sigs[i]
    vec = [-(s-1)*z]
    zbin = bin(z)[2:].zfill(256)
    assert len(zbin) == 256
    zbin = zbin[::-1]
    for i in range(256):
        tmp = (2^i) * (r + (2*int(zbin[i])-1) * s) % (CURVE.q)
        vec.append(tmp)
    main_mat.append(vec)
mat = matrix(ZZ, main_mat).T

M = block_matrix(ZZ, [[UL, UR], [mat, DR]])
M = M.LLL()
for row in M:
    if row[6] == 1 and set(row[7:]).issubset([0, 1]):
        print('Find solution!')
        d = int(''.join(list(map(str, row[7:][::-1]))), 2)
        print(d)
        break

key = sha256(str(d).encode()).digest()[:16]
fake_cipher = AES.new(key, AES.MODE_ECB)
prefix = b"Congrats! This is your flag: "
nonce = fake_cipher.decrypt(xor(prefix[:16], c[:16]))[:8]
cipher = AES.new(key, AES.MODE_CTR, nonce=nonce)
print(cipher.decrypt(c))

Find solution!
113469799004661487320247409448796883146298153010773207076143627146899378821364
b'Congrats! This is your flag: TSJ{who_needs_gaussian_elimination_when_you_have_LLL?_https://github.com/jonasnick/ecdsaPredictableNonce}'

0x01 Codegate2022 Prime-Generator

Category: Crypto
Solve:10/141

源码：

from Crypto.Util.number import *
import os

BITS = 512
UPPER_BITS = 296
LOWER_BITS = BITS - UPPER_BITS

UPPER = bytes_to_long(os.urandom(UPPER_BITS // 8)) << LOWER_BITS
FLAG = b'codegate2022{this_is_a_sample_flag}'

def menu1():
    while True:
        lower = bytes_to_long(os.urandom(LOWER_BITS // 8))
        p = UPPER | lower
        if isPrime(p): return lower

def menu2():
    p = UPPER + menu1()
    q = getPrime(512)
    e = 0x10001
    n = p * q
    return n, pow(bytes_to_long(FLAG + b'\x00' + os.urandom(128 - 2 - len(FLAG))), e, n)

while True:
    print("1. Generate 10 random primes (only lower bits)")
    print("2. Encrypt a flag")
    idx = int(input("> "))
    if idx == 1:
        print("How many? (Up to 10)")
        num = int(input("> "))
        for _ in range(min(10, num)):
            print(menu1())
    elif idx == 2:
        n, c = menu2()
        print(f"n : {n}")
        print(f"c : {c}")
UPPER = bytes_to_long(os.urandom(UPPER_BITS // 8)) << LOWER_BITS

可以看出这个题目给了两个功能：menu1和menu2，menu1会生成一个形如UPPER*(2^216) + lower的素数，并返回它的低216bits，其中UPPER在每次交互的时候是不变的(296bits)。menu2会调用menu1生成一个如上格式的素数作为p，再随机生成一个512bit的q，进行RSA加密，并返回n和密文c。

乍一看思路其实很清晰，我们只需要拿到UPPER即拿到了p的高位，即可用partial p attack对n进行分解。那么如何从无限多的低位中拿到UPPER呢？

这里我们用到了一个有用的结论，因为UPPER*(2^216) + lower是一个素数，那么对于比较小的素数p来说，我们有：

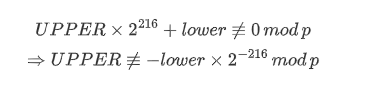
只要我们拿到足够多的lower并且根据这个事实筛选掉不符合条件的值，我们就可以得到UPPER mod p的值了，之后我们利用CRT即可恢复UPPER。因为UPPER为296bits，那么前50个素数（不包括2）即可作为p来使用。

因为比赛已经结束，赛后复盘并没有在服务器上搭建环境，本地模拟了大致的流程：

模拟流程及exp:

from Crypto.Util.number import *
import os

BITS = 512
UPPER_BITS = 296
LOWER_BITS = BITS - UPPER_BITS

UPPER = bytes_to_long(os.urandom(UPPER_BITS // 8)) << LOWER_BITS
FLAG = b'codegate2022{this_is_a_sample_flag}'

def menu1():
    while True:
        lower = bytes_to_long(os.urandom(LOWER_BITS // 8))
        p = UPPER | lower
        if isPrime(p): return lower

def menu2():
    p = UPPER + menu1()
    q = getPrime(512)
    e = 0x10001
    n = p * q
    return n, pow(bytes_to_long(FLAG + b'\x00' + os.urandom(128 - 2 - len(FLAG))), e, n)

def check_fine(reminder):
    flag = 0
    for x in reminder:
        if len(x) > 1:
            flag = 1
            break
    return flag

sieve = [3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229]
reminder = [[x for x in range(k)] for k in sieve]
constant = 2^216

while check_fine(reminder):
    lowers = [menu1() for i in range(10)]
    for lower in lowers:
        for i in range(len(sieve)):
            RHS = (-lower * inverse(constant, sieve[i])) % sieve[i]
            if RHS in reminder[i]:
                reminder[i].remove(RHS)
crt_rem = []
for v in reminder:
    crt_rem.append(v[0])
upper = crt(crt_rem, sieve)

e = 0x10001
n, c = menu2()

P.<x> = PolynomialRing(Zmod(n))
f = x + upper * constant
root = f.small_roots(X=constant, beta=0.4, epsilon=5/32)[0]
p = int(f(root))
q = n // p
assert p * q == n
phi = (p-1)*(q-1)
d = int(inverse(e, phi))
m = int(pow(c, d, n))
print(long_to_bytes(m))

b'codegate2022{this_is_a_sample_flag}\x00\xef\x10v\xdfn\x11\x89Z\x18\x1f\xddx\xcd\x9b\x82\xdd\x1f\x8bx\xaa\xec\x93U\xa4\x7f\xd9\xe9r\xb9\xb0wk-\x9d\xe5\x88\td\x8d\x94\x7f\xdc\xad\xb1\xf3\xb1\xb1\xc3\xd3r\x03\\\x8f<\x13A}@\x98h\xcb/\x82\xeewU\x1b\xcf}]\xddZ\xc8X\xe9O\xce\x9d\xd2<+\xab\xa5\x05+\xa7\xca\x1f\x0c\xd5L'

0x02 小结

TSJCTF中的那道nonce相关题目其实是真实的案例改编的，他原本来自github.com/obscuren/secp256k1-go，一个golong的密码学库，其中就选择了这样的bad nonce，当然这个库现在已经404了。总而言之这些题目是比较新颖和有趣的，无论是新的ecdsa的nonce问题还是巧用crt的新奇思路，都让我学到了很多知识，国际赛的质量还是挺高的。

我正在「Funny Web CTF」和朋友们讨论有趣的话题，你⼀起来吧？

0x03 参考：

https://blog.maple3142.net/2022/02/28/tsjctf-2021-writeups/#signature

K	k0uaz foniw师傅提到的setfge当在类的字段名成是age时不会自动调用。因为获取
	Yukong 🐮皮
H	HHHeey 好的，谢谢师傅的解答
	Article_kelp a类中的变量secret_class_var = "secret"是在merge
H	HHHeey secret_var = 1 def test(): pass