Brief
很新颖的一道题目,比赛时花了将近一整天的时间做了出来(没抢到血 qaq,带哥们太猛了)。虽然 XCTF 的分站赛主办方都会公布 writeup,但还是很想记录并顺手分享一下我自己在解这道题目时的整个思考过程。尤其是这几年 CTF 中逆向方向其实已经把基础考点都考的差不多了,现在更多的是在创新性上下文章,分析程序的思路就显得更重要了。
在上手做这道题目之前首先需要对 C++ 的模板及泛型编程有个大概的了解,这里贴一份入门介绍:
我将分几个 stage 来介绍自己的解题过程。
Stage 1: refactoring
拿到一个 .hpp 文件,里面有 2000 余行嵌套的 template definition,然后是一个 struct Nagi ,里面有一个 static member buf 和一个 static function GetFlag, 最后是声明了这个 buf 的具体值。
GetFlag 一看就是 RC4 密码算法, 而且 buf 就是 ciphertext. 因此现在缺的就是正确的 key 了,而想要得到正确的 key 还需要 过掉 RT 处的 check
template<typename...U>
struct Nagi {
static char buf[108];
static const char* GetFlag() {
if (RT<U...>::value == false) {
return "I don't know the flag, ask some else!";
}
int key[] = { HA<U>::value... };
int S[256];
int i, j = 0, t;
for (i = 0; i < 256; i++) { S[i] = i; }
for (i = 0; i < 256; i++) {
j = (j + S[i] + key[i % sizeof...(U)]) & 0xff;
t = S[i], S[i] = S[j], S[j] = t;
}
i = j = 0;
for (int k = 0; k < 107; k++) {
i = (i + 1) & 0xff;
j = (j + S[i]) & 0xff;
t = S[i], S[i] = S[j], S[j] = t;
buf[k] ^= S[(S[i] + S[j]) & 0xff];
}
return buf;
}
};
key 由 HA<> template 类型提供, 而该类型根据其 template parameter 参数的不同又定义为 CM 类型。
CM<> 是对 int 的封装,因此将之重命名为 IntW,同时也发现 CM<> 附近也有很多类似的简单 template 声明,也将这些 template 根据其含义进行重命名。
这时发现这题还挺巧妙的,出题人通过 template specialization 实现了逻辑上的很多运算,举例如下
typedef BoolW<false> FalseW;
typedef BoolW<true> TrueW;
template <typename T>
struct Not : BoolW<!bool(T::value)>
{
};
template <typename...>
struct And : TrueW
{
};
template <typename T>
struct And<T> : T
{
};
template <typename T, typename... U>
struct And<T, U...> : Ternary<bool(T::value), And<U...>, T>::type
{
};
template <typename T, typename... U>
struct Xor : Ternary<bool(T::value), Not<Xor<U...>>, Xor<U...>>::type
{
};
有些运算仅仅去审计是不太好确定的,这时可以定义一下相应的类型然后看看结果
int main() {
cout << Xor<TrueW, FalseW, TrueW>::value << endl;
}
通过审计 + 测试,可以大概把前 254 行的 template 声明完全看懂,但随后几个声明过于复杂,比赛时我是没有看懂。此时进入下一个 stage,即理解这一堆声明是在干什么
Stage 2: understanding
再次梳理程序的结构
- 0~254: 基本的 template,嵌套层级较少,简单,可以完全看懂,视作白盒
- 255~335: 复杂 template,后者嵌套前者,复杂,视作黑盒
- 336~375: 共 8 个声明,都依赖于 HN 这个 template,记作
Op_0 ~ Op_7 - 376~1910:大量的嵌套,但仅使用了 336~375 处定义的 template,且都是
Add<...>的结构 - 1911~2101:共有 32 个声明,对 376~1910 中定义类型的简单引用,记作
C_0 ~ C_{31} - 2102~2262:同样是后者依赖于前者 template 定义,只不过结构相当统一,都是
And<Pre, IsSame<C_n, Op_m<Float:type>>的结构,同样共有 32 个 - 2263~2287: 8 个声明,对 parameter T 进行判断然后映射到不同的
IntW
发现
-
8 和 32 这几个数字在不同的程序段落中出现了好几次,一定有特殊的含义。
-
在 0~254 中出现的类型修饰符有
const, float/int, &3 种,而2**3 == 8
这时即推测,出题人是用这三类修饰符代表了三个 bit,然后定义了 GF(8) 中的乘法和加法运算
同时
-
再去看 336~375 处定义的 8 个 Op,每个 Op 都是由内置的一个类型与传入的类型 T 运算再结合 HN 得到最终结果。考虑到出题人并没有恶心到把 template def 打乱,因此大胆猜测这里面内置的类型就代表了 0~7 8 个数字
-
376~1910 中定义的都是
Add<Op(x), Op(y)...>这样的操作,并且在嵌套之后共有 32 个Op(x)相加
不难想到这是矩阵点乘的一个计算过程,出题人实际上就是用 template 的嵌套定义实现了有限域内矩阵的点乘运算
类型 -> 数值的映射如下所示
m = {
0: "int",
1: "float",
2: "const int",
3: "const float",
4: "int &",
5: "float &",
6: "const int &",
7: "const float &"
}
Stage 3: solving
确定本原多项式
此时,由于是有限域内的运算,还需要确定使用的本原多项式具体是什么
由于 HN 过于复杂,此时采用黑盒的办法来确定
这里介绍一个 trick,llvm 提供了很多 API 可以让我们自定义程序来分析程序,同时也提供了 Python 的封装,使用就非常方便了
可以使用 clang API 来获得一个复杂声明的最终变量类型
one.cpp
#include "nagi.hpp"
int main() {
Op7<float &>::type a;
}
main.py
import clang.cindex
from clang.cindex import *
Config.set_library_file("libclang-10.so")
def walk(cursor: Cursor):
l: SourceLocation = cursor.location
if cursor.kind == CursorKind.VAR_DECL and "one.cpp" in str(l.file):
t: Type = cursor.type
t = t.get_canonical()
print(t.spelling)
for child in cursor.get_children():
walk(child)
m = {
0: "int",
1: "float",
2: "const int",
3: "const float",
4: "int &",
5: "float &",
6: "const int &",
7: "const float &"
}
rm = {}
for k, v in m.items():
rm[v] = k
index = clang.cindex.Index.create()
walk(index.parse("./one.cpp").cursor)
因此得知 Op7(float &):type -> float ,即在该有限域下 5*7 = 1,即可确定本原多项式
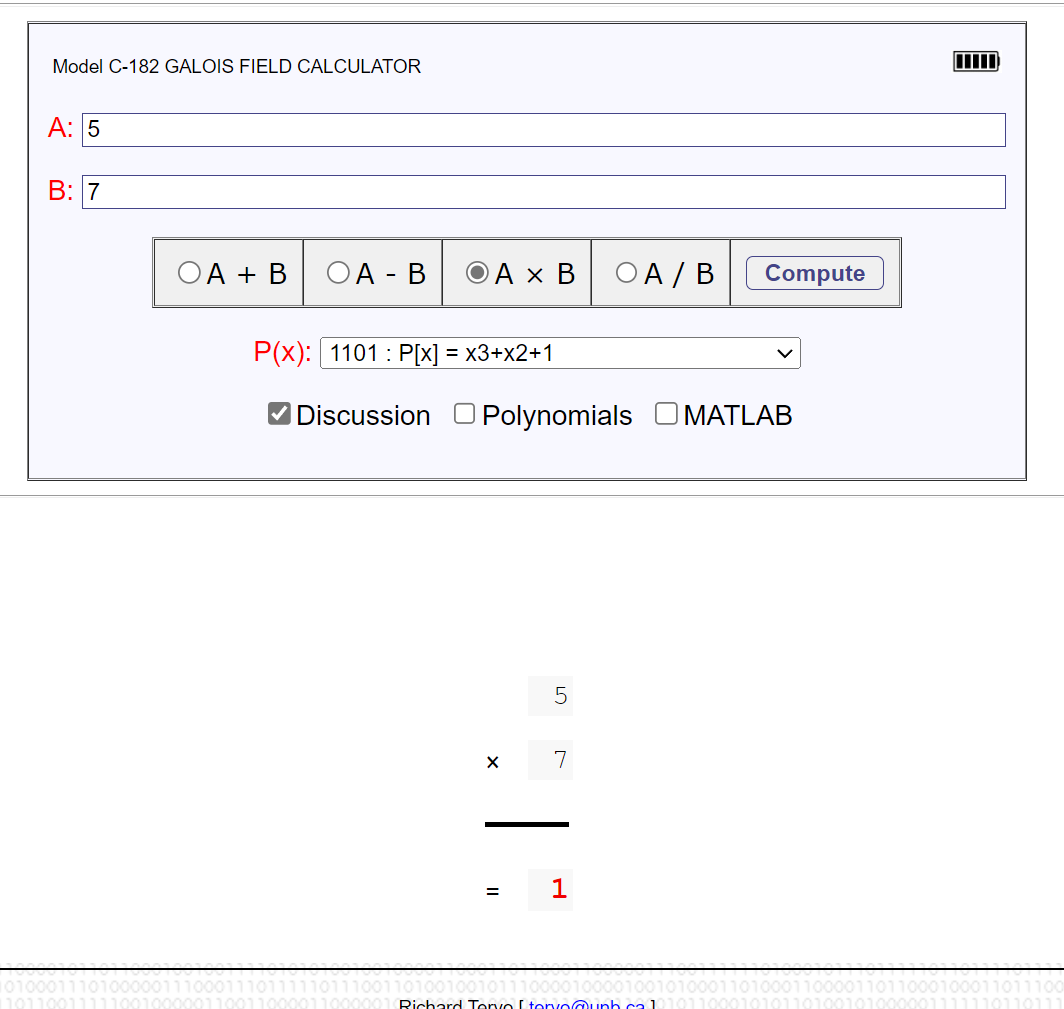
求解
大致思路就是分析 376~1910 行间的 template 声明,从中提取加密矩阵和运算结果,然后在 Galois 域上进行运算求解
import numpy as np
import galois
from typing import List, Mapping, Tuple
import clang.cindex
from clang.cindex import *
Config.set_library_file("libclang-10.so")
ENTRY_FILE = "./one.cpp"
def get_template_classes():
template_classes: Mapping[str, Cursor] = {}
def walk(node: Cursor):
if (node.kind == CursorKind.CLASS_TEMPLATE):
template_classes[node.spelling] = node
for child in node.get_children():
walk(child)
index = clang.cindex.Index.create()
walk(index.parse(ENTRY_FILE).cursor)
return template_classes
def get_template_ref_tokens(cursor: Cursor) -> List[Token]:
return [token for token in cursor.get_tokens() if token.cursor.kind == CursorKind.TEMPLATE_REF]
TEMPLATE_CLASSES = get_template_classes()
def op_val(op: Token) -> int:
return int(op.spelling.strip('Op'))
def extract_all() -> Tuple[List, List]:
resutls: List[int] = []
conditions: List[List[int]] = []
next_name = 'RT'
# next_name = 'II'
for _ in range(32):
template = TEMPLATE_CLASSES[next_name]
tokens = get_template_ref_tokens(template)
for i, token in enumerate(tokens):
token: Token
if token.spelling == "IsSame":
pivot = i
condition_template = TEMPLATE_CLASSES[tokens[pivot+1].spelling]
resutls.append(op_val(tokens[pivot+2]))
conditions.append(parse_top_condition_template(condition_template))
# update
if len(tokens) == 4:
break
else:
next_name = tokens[1].spelling
return conditions, resutls
def parse_top_condition_template(top_template: Cursor) -> List[int]:
for token in top_template.get_tokens():
token: Token
if token.cursor.kind == CursorKind.TEMPLATE_REF:
sub1_template = TEMPLATE_CLASSES[token.spelling]
break
def parse_sub_template(sub_cursor: Cursor) -> List[int]:
tokens = get_template_ref_tokens(sub_cursor)
left_ints = [op_val(tokens[1]), op_val(tokens[2])]
right_ints = [op_val(tokens[-2]), op_val(tokens[-1])]
if len(tokens) == 5:
return left_ints + right_ints
else:
next_cursor = TEMPLATE_CLASSES[tokens[-3].spelling]
return left_ints + right_ints + parse_sub_template(next_cursor)
return parse_sub_template(sub1_template)
conditions, results = extract_all()
def rc4(key):
data = "\xb0\x0d\x1f\x0e\x2a\x27\x08\xd4\x1b\x8a\xf9\xde\x67\x86\x95\x80\x4f\x92\xca\xa1\x70\x2c\x53\xae\xd7\x4e\xf2\x86\x4f\x37\x03\xdc\xbe\xf2\xc4\x0e\x7c\x8f\x8a\x00\x09\x93\xf0\xd0\xf3\x37\xd4\x7e\x6f\x83\x6d\x3e\x16\x99\x63\x25\x7a\x3c\x30\x51\xaf\xf6\x3e\xc5\x0f\xc8\x93\xeb\x4f\x6b\xbd\xc2\xa1\x96\x2b\x4e\xc4\xca\x91\xcd\x70\xc2\x24\xe8\xa2\x92\xbe\x1e\xea\x48\xf9\x16\xb0\x78\x00\x6b\x7c\x95\xb1\xa0\xcb\xf7\x06\xaf\x4d\xe8\x96"
key = key
S = [i for i in range(256)]
j = 0
out = []
# KSA Phase
for i in range(256):
j = (j + S[i] + key[i % len(key)]) % 256
S[i], S[j] = S[j], S[i]
# PRGA Phase
i = j = 0
for d in data:
i = (i + 1) % 256
j = (j + S[i]) % 256
S[i], S[j] = S[j], S[i]
out.append(chr(ord(d) ^ S[(S[i] + S[j]) % 256]))
print(''.join(out))
gf = galois.GF(2**3, irreducible_poly=0b1101)
conditions = gf(conditions)
results = gf(np.array(results).T)
plains = np.linalg.inv(conditions).dot(results)
reflect = [3, 5, 7, 11, 13, 17, 19, 21]
forward = [reflect[int(i)] for i in plains]
rc4(forward)
m = {
0b0: "int",
0b1: "float",
0b10: "const int",
0b11: "const float",
0b100: "int &",
0b101: "float &",
0b110: "const int &",
0b111: "const float &"
}
types = []
for i in plains:
types.append(m[int(i)])
print(', '.join(types))
得到 flag ACTF{y3s_my_nam3_i5_N4NagiIJfRKfS1_fRfKiS0_S0_S1_S2_S3_S1_RS3_ifS2_S2_RifS0_S1_S4_fS0_S4_ifS3_S0_S0_S2_iEE}
同时咱也把重命名后的 nagi.cpp 在 gist 上贴了一份,dalao 们复现的时候可以参考一下
 跳跳糖
跳跳糖

